Инструмент трассировки содержит много средств для создания проводников. Два трассировщика могут использоваться в array-based проекте, для соединения смежных ячеек. Maze-router выполняет отдельные проводники. Для выполнения шин доступен River-router. Sea-of-gates router обрабатывает много проводников с произвольным соединением. Наконец, есть шесть экспериментальных маршрутизаторов, основанных на A*, Ли, Мура (Lee/Moore) -алгоритмах .

Непроведенные трассы

Все non-stitching routers рассматривают непроведенную трассу, как тонкую дугу которая может соединить любые два компонента. Создание "rats nests" этих дуг формирует графическую спецификацию, которую может использовать трассировщик. Непроведенная трасса описана в Универсальной Технологии (см. раздел 7-6-3). Чтобы создать такую, используйте команду Get Unrouted Wire (в меню Tools / Routing).

Затем используйте стандартные команды проводного соединения, чтобы провести непроведенный проводник. Другой способ получить непроведенные связи состоит в том, чтобы выбрать все, или часть существующей трассы и использовать команду Unroute.

Другой способ получить непроведенные дуги для маршрутизатора состоит в том, чтобы использовать команды Copy Routing Topology и Paste Routing Topology. Они копируют топологию цепи с одной ячейки ("copied" ячейка) к другой ячейке ("pasted" ячейка). Скопированная ячейка должна быть должным образом трассирована. Команда Paste Routing Topology использует имена узла и дуги, чтобы связать две ячейки.

Предпочтения

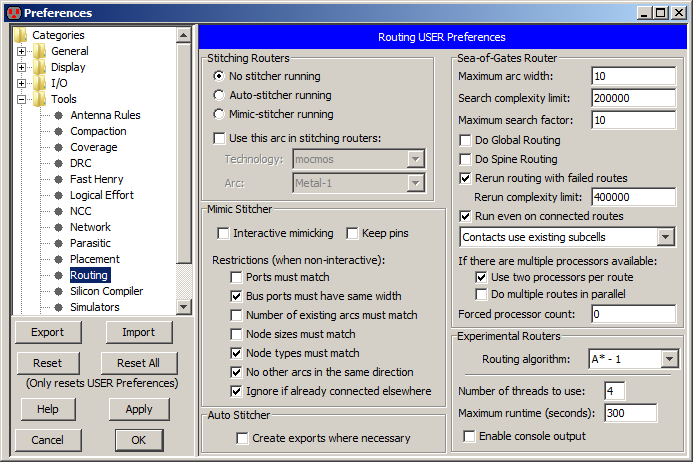
Routing Preferences (в меню File / Preferences..., "Tools" section, "Routing" tab) управляют всеми трассировщиками. Раздел в верхнем левом применяется к двум сшивающим трассировщикам (Mimic and Auto). Определенные разделы применяются к определенным маршрутизаторам (см. Раздел 9-6-3 для Mimic Stitcher, Раздел 9-6-2 для Auto Stitcher, и Раздела 9-6-6 для маршрутизатора Sea-of-Gates).

Экспериментальные трассировщики

Шесть экспериментальных трассировщиков доступны в подменю Experimental Routers. Три из них основаны на алгоритме A*, и три основаны на алгоритме Lee/Moore. В каждом случае первый является самым стабильным из всех.